Ofqual routinely analyse how attainment gaps for students with protected characteristics and different socio-economic status vary over time. This interactive report presents the results of the analysis for the period 2018 to 2023 for GCSEs, A levels (referred to here as General Qualifications, GQ) and a subset of Vocational and Technical Qualifications (VTQs).
Gaps in 2023 results are compared primarily with 2022, when exams returned after the pandemic (though with a package of support for students), and with 2019, the last year before the coronavirus (COVID-19) pandemic.
Executive summary
Ofqual routinely analyses how attainment gaps for students with different protected characteristics and socio-economic status vary over time, for GCSEs and A levels (referred to here as general qualifications (GQ)) and a subset of vocational and technical qualifications (VTQ) (see: GQ 2020, VTQ 2020; GQ 2021; VTQ 2021, GQ & VTQ 2022). This year, results are published in an interactive format on Ofqual Analytics. This statistical analysis allows users to explore how differences in results between groups of students with different protected characteristics and socioeconomic status have changed in 2023 in relation to previous years.
The methodology used in this analysis allows us to identify and quantify the changes that have occurred. It is difficult, however, to identify the causes of any of these changes. There are likely to be many possible causal factors, including existing societal differences and the impact of the pandemic on teaching and learning. Analysis from 2018 and 2019 shows that differences in results existed in pre-pandemic times and can vary from year to year. Many of the findings reported here are likely to reflect normal fluctuations in outcomes from one year to the next.
As in previous analyses, in addition to presenting the descriptive analysis of the raw differences in results between groups of students, Ofqual used a multivariate analytical approach. This allows us to explore the impact on overall results of each feature separately while controlling for other features. This is important because we know that there are relationships between different features (for example, ethnicity and first language).
We used regression modelling to estimate differences in results for groups of students after controlling for other variables. The variables analysed were:
- ethnicity
- gender
- special educational needs and disabilities (SEND) status
- free school meal (FSM) eligibility (a measure of deprivation)
- Income Deprivation Affecting Children Index (IDACI) score
- prior attainment
- first language (GQ only)
- region (GQ only)
- centre type (GQ only) according to JCQ categories
For most of the above variables, the largest group is used as a comparator, and all other groups are compared to that. For example, for ethnicity, we use white British as the comparator as it is the largest group. We compare students in other ethnic groups with white British students of the same gender, SEND status, FSM eligibility, IDACI score, prior attainment, first language, region and centre type. We estimate the results of the ‘average’ student, that is, a student who falls into the comparator group for every variable, and can then examine the impacts of each of the other groups separately.
In this analysis, results for 2023 are presented alongside those for the period from 2018 to 2022. This report focuses on 2 comparisons. We compare results in 2023, when exams were held with the aim to return to pre-pandemic grading, with results in 2022, when exams returned following the pandemic with a package of support for GCSE and A levels and adaptations (for GCSE, A levels and VTQs) including lenient grading. We also compare results in 2023 with results in 2019, the last year that summer exams were taken before the pandemic.
Analysis of results for 2018 to 2023 are shown in the interactive charts and accompanying data tables. Given the exceptional circumstances under which grades were awarded in 2020 and 2021, any adaptations for qualifications and the package of support in place for GCSE and A levels in 2022, any comparison with these years should be treated carefully.
General qualifications
For GCSEs and A levels we analysed 3 outcome measures:
- grade achieved
- the probability of attaining grade 7 and above for GCSE, or grade A and above for A level
- the probability of attaining grade 4 and above for GCSE, or grade C and above for A level
We used a set of criteria to identify changes we considered to be ‘notable’, those changes that we believe go beyond normal year-on-year fluctuations. These changes are drawn out in the interactive report. Of the many comparisons between groups of students presented in our modelling, the majority showed no notable change in 2023, with respect to 2019 and 2022.
A level
For A level in 2023, the modelling showed that the grade for an average student was a grade C (3.47 on a numeric scale of 0 to 6, where 0 was ungraded and 6 was A*). The probability of an average student attaining grade A and above was 18.3%, and the probability of them attaining grade C and above was 80.7%. The average student’s grade and probabilities of attaining grade C or above and grade A or above in 2023 were broadly in line with 2019 and lower than in 2022. This is to be expected, given the intended staged return to pre-pandemic grading over the last 2 years.
Some groups showed notable changes on all 3 of the above outcome measures when controlling for other variables. We found the following notable changes on all 3 outcome measures:
-
In 2023, students in further education colleges had lower outcomes than students in academies. The difference of 0.45 of a grade (almost half a grade) was 0.35 grade wider than in 2019, but broadly in line with 2022.
-
Students in sixth form colleges had lower outcomes than students in academies. The differences of 0.10 of a grade reversed the difference in 2019 when sixth form students had higher outcomes than academy students.
GCSE
For GCSE in 2023, the modelling showed that the grade for an average student was a high grade 4 (4.90 on a scale of 0 to 9, using the numeric grades). The probability of an average student attaining grade 7 and above was 16.0%, and the probability of them attaining grade 4 and above was 80.1%. The average student’s grade and probabilities of attaining grade 4 or above and grade 7 or above were similar to 2019 and lower than in 2022, as expected.
Some groups showed notable changes on all 3 outcome measures relative to demographics-matched students in the comparator groups:
-
Students in independent schools had higher outcomes than students in academies. The difference of 1.6 grades was 0.2 grade narrower than in 2019, but has widened slightly by 0.1 grade since 2022. Given that the gap for probability of attaining a 7 (or above) narrowed, this increase has to do with the probability of attaining a 4 (or above), which is slightly larger than in 2022, but still lower than in 2019.
-
White Gypsy and Roma students had lower outcomes than white British students. The difference of 0.92 grade was 0.28 grade narrower than in 2019.
-
Chinese students had higher outcomes than white British students. The difference of 1.12 grades was 0.22 grade wider than in 2019.
-
FSM-eligible students had lower outcomes than FSM-ineligible students. This difference of 0.51 grade was 0.13 grade wider than in 2019, though the change with respect to 2022 was not notable.
-
Male students had lower outcomes than female students. The difference of 0.28 grade was 0.12 grade narrower than in 2019.
Vocational and technical qualifications
For vocational and technical qualifications (VTQs) analysis, we focused on national qualifications used alongside GCSEs and A levels in schools and colleges and included in the Department for Education’s (DfE’s) performance tables – specifically Level 1, 1/ 2 and 2 Technical Awards and Technical Certificates, and Level 3 Applied Generals and Technical Level qualifications. Unlike GCSEs and A levels, these VTQs have different structures and grade scales. The analysis, therefore, looks at the probability of achieving the top grade, that is the highest grade that can be achieved in each qualification.
In the majority of cases, no notable changes over time in the relative average probabilities of achieving top grades between different groups of learners were observed.
For level 1, 1/ 2 and 2 Technical Awards and Technical Certificates the modelling showed that the probability of an average student attaining the top grade was 2.1% and 1.9% respectively in 2023. This is lower than in 2022.
There were no notable changes for level 1 and 2 Technical Awards, whereas for level 2 Technical Certificates notable changes were seen with respect to prior attainment. In 2023, the gap between students with low and very low prior attainment when compared to those with medium prior attainment narrowed 6 and 5 percentage points respectively compared to 2019. Students with low prior attainment were about as likely as students with medium prior attainment to obtain top grades in 2023, while students with very low prior attainment were on average 1% less likely to achieve top grades.
Additionally, there were notable changes relating to some groups with different ethnic backgrounds. However, the numbers of students in these groups are relatively small and so these findings should be treated with caution.
For level 3 VTQs the modelling showed that the probability of an average student attaining the top grade in Applied Generals and Tech Level qualifications was 2.9% and 4.6% respectively in 2023. This is similar to 2019 and lower than in 2022.
For Applied Generals there were no notable changes, whilst for Tech Level qualifications notable changes were highlighted for some ethnic background groups. The numbers of students in these groups are relatively small and so these findings should be treated with caution.
For any feedback on these graphs, please contact [email protected].
Return to the Ofqual Analytics home page.
If you need an accessible version of this information to meet specific accessibility requirements, please email [email protected] with details of your request.
Introduction
Since 2020 Ofqual has analysed how results gaps in relation to protected characteristics and socioeconomic status vary over time for GCSE, A levels and VTQs included on Performance Tables (see: GQ 2020, VTQ 2020; GQ 2021; VTQ 2021, GQ & VTQ 2022.
This equalities analysis has been repeated for 2023, which saw the return to pre-pandemic grading, although with a degree of protection to recognise the disruption that students faced. In 2023 national results were lower than in 2022, and comparable to 2019 results, the last year that summer exams were taken before the coronavirus (COVID-19) pandemic.
It should be noted that differences in attainment between groups of students can have multiple and complex causes. It is not possible to disentangle causal factors such as the effects of teaching and learning from the impacts of different awarding arrangements put in place during and after the pandemic. Therefore, while we aim to report differences in attainment associated with students’ characteristics where they appear to exist, we do not speculate on their underlying causes. A degree of change is expected in any given year, and some of the findings reported here are likely to reflect normal fluctuations in outcomes from one year to the next.
Background
As part of a two-year, two-step plan to return to normal grading arrangements after the pandemic, in summer 2023 GCSEs and A levels returned to pre-pandemic standards, with national results in 2023 broadly in line with those in 2019. Protection was built into the grading process to recognise the disruption that students had faced.
Further information is available on the Ofqual website, in the Ofqual student guide 2023, and in our blog 10 things to know about GCSE, AS and A level grades .
In 2023 there was also a return to all exams and formal assessments across VTQs . For VTQs, changes to the qualifications available and entry patterns mean that even though the approach to grading in 2023 was similar to 2019, the pattern of grades achieved may look different from 2019. Additionally, many vocational and technical qualifications allow students to take assessments throughout their course, so results from assessments taken in earlier years may have been used when determining 2023 grades.
Examinations and assessments were re-introduced in summer 2022, following disruption due to the pandemic in 2020 and 2021. A package of support for students, including adaptations to assessment and more lenient grading, were put in place for GQs and VTQs. Outcomes in 2022 were lower that in 2021, but higher than pre-pandemic, hence any comparison with 2022 results should be treated carefully.
In 2020 and 2021, with the cancellation of exams, arrangements for awarding were different due to the impacts of the pandemic. Grades for GQ were based primarily on Centre Assessment Grades (CAGs) in 2020 and Teacher Assessed Grades (TAGs) in 2021. For VTQ, many assessments were adapted, delayed, or replaced by CAGs in summer 2020 or TAGs in summer 2021. In 2020 and 2021, when GCSE, AS and A level grades were determined by teachers, national outcomes were higher than prior to the pandemic.
Analytical approach
Alongside descriptive statistics on the differences between groups of students, the report focuses on the result of multivariate modelling, which is more informative than simple descriptive breakdowns between different characteristics. Multivariate analyses allow the effect of a characteristic to be considered while controlling for the impacts of other variables. For example, we can compare the effect of being female vs being male on outcomes, while holding prior attainment and ethnicity constant. If there are no differences in female vs male effects, we can conclude that differential performance in female students compared to male students was associated with other factors – such as a higher level of ability and/or ethnicity – and not their gender.
Analysis of the differences between groups of students in 2018 and 2019 tells us that such differences in exam outcomes existed in pre-pandemic times and can vary from year to year even in normal times. By comparing changes in these differences between 2023 and 2019 and between 2023 and 2022, against changes between 2019 and 2018, we identified the ‘notable’ changes between 2023 and 2019 and those between 2023 and 2022. We used a series of criteria (see Methodology sections below) to identify changes that we considered to be practically significant while taking into consideration normal between-year fluctuations. In this paper, we use the word ‘notable’ to refer to between-group differences that met these criteria. The term ‘notable’ is not intended to convey any judgement of the importance of the change in question.
The data used in this analysis included data collected from awarding organisations by Ofqual as well as student-level background information from the Department for Education. Data was matched using students’ names, date of birth and gender. A set of explanatory variables were included in the models. For each variable, a reference category was chosen. This was usually the largest category (for example, white British is used for ethnicity as this group represents the largest proportion of cases) or the category that represents the middle of an ordered group (for example, medium is the reference category for prior attainment, the others being very low, low, high and very high). When comparisons are made in the results section below, each category is compared to the reference category, after controlling for other explanatory variables. Some variables were used in the GQ analysis only due to differences in availability of data.
The variables included in the models, along with their reference categories in brackets, were:
- ethnicity (white British)
- gender (female)
- special educational needs and disabilities status (no SEND)
- free school meal (FSM) eligibility as a measure of deprivation (not eligible)
- IDACI score (medium)
- prior attainment (medium)
- first language – included for GQ only (English)
- region – included for GQ only (south-east)
- centre type (the type of school or other educational setting in which the qualification was taken) – included for GQ only (academies)
We included a measure of prior attainment in this analysis. For GCSE, Level 1, Level 1/ 2 and Level 2 vocational and technical qualifications, prior attainment was from key stage 2. For A level and Level 3 VTQ qualifications, GCSE prior attainment was used. Prior attainment is the stronger predictor of achievements in these qualifications and including it in the models gives a more accurate interpretation of the effect size of other variables. As the model quantifies the effect of each variable after controlling for prior attainment, among other variables, the effects relate to the differences that the variables would have made since candidates took their key stage 2 or GCSEs, rather than the differences that the variables may introduce across an entire school career. A multilevel modelling approach was used to take account for the hierarchical structure of the data that results in clustering. Clustering means that, for example, the students within a school or college might be more likely to have similar results to each other compared to other students from the population, because of factors that are common to that particular school or college. Clustering within schools and colleges was accounted for in both the GQ and VTQ models. In addition, the GQ models took into account clustering within students (across multiple subjects) and within subject.
This analysis focuses on GCSEs and A levels and the subset of VTQs included in the DfE’s performance tables, specifically Level ½ Technical Awards and Technical Certificates, and Level 3 Applied Generals and Technical Level qualifications. The scope of VTQ qualifications included in this analysis is slightly different to the analysis published in previous years due to changes to the data collection. For this reason and due to improvements to methodology, the current report should be seen as the most up to date source of information for both GQ and VTQ.
General Qualifications Methodology
Data
Data collected from awarding organisations on students' grades, gender, prior attainment, centre type and region was matched to extracts from the National Pupil Database (NPD) containing FSM status, SEND status, language, ethnicity and IDACI score from the year of awarding. Students who could not be uniquely matched or who could be uniquely matched but who had no relevant information in the NPD were marked as missing data on the relevant variable. Missing data rates are given in Appendix B. Data on prior attainment and the background variables are missing to varying degrees and not at random.
Tables in Appendix B show the extent of missing data for each background variable used in our analysis. There was no missing data on the region and centre type variables and nearly none on gender, but data on prior attainment and other background variables were missing to varying degrees. Also, data was missing not at random, as the extent of missing data varied by centre type.
Missing data on the background variables is most likely the result of schools and colleges not returning the DfE School census. Missing data on KS2 prior attainment most likely reflects the fact that some students did not sit the KS2 tests for a variety of reasons, including being absent from school at the time of the tests, attending independent schools at KS2, or attending school outside of England at the time of the tests. Missing data on GCSE prior attainment has a similar cause: some students did not take GCSEs at 16. As with any analysis involving the merging of datasets, missing data can also be caused by data matching problems.
Missing data can be problematic, particularly where it is systematic rather than random. It raises questions about whether the findings from the modelling about the known categories apply to the whole student population, whether those findings would still hold if the unknown information were known, and whether the unknown categories could effectively be treated as proxies for some centre type(s) due to some centre types having much higher proportions of missing data.
Nonetheless, the comparisons of interest here concern not so much the between-group differences within each year, but rather any changes in between-group differences in 2023 compared with previous years. As is evident from the table in Appendix B, the missing data rates and patterns are comparable across the 6 years, so we can reasonably assume the subgroups are comparable in terms of ‘missingness’, although we note some factors driving instability in the FSM eligibility measure below as well as some changes in outcomes of some groups with missing data. That is to say, while we might interpret the estimates of the differences between groups within each year cautiously, any change to those differences between years can be interpreted as a change in relative outcomes for different subgroups.
Where data was missing, we included the categories in the model as ‘unknown’ groups. We did observe some notable differences (see notable difference methodology below) between some of these ‘unknown’ groups and the reference groups, which could indicate some degree of systematic change underlying the missing groups. The outcomes for the unknown categories are included in the charts and tables in the results and appendices. We observed some notable changes between 2023 and either 2019 or 2022 on at least one outcome measure for the unknown categories for prior attainment, ethnicity, IDACI, major language and FSM at both GCSE and A level.
In terms of data limitations, it is also worth noting that the proportion of students eligible for FSM increased between 2018 and 2023, due to an arrangement related to the roll-out of Universal Credit and, since 2020, the economic impact of the Covid-19 pandemic (Julius and Ghosh, 2022). This increase was also reflected in the GCSE equalities dataset, with the proportion of entries by FSM-eligible students increasing year on year in 2018 to 2023. The subgroups under the FSM status variable were therefore less stable across the years than other variables included in the analysis. To ensure like-for-like comparisons, we built an equalities dataset from the matched data for each qualification level consisting of data for:
- students who by 31 August of the respective year were at the target age of the qualification level of their entries (16 for GCSE, 18 for A level) subjects examined under the same specifications in 2018 to 2023 (this meant in effect only reform phase 1 and phase 2 subjects/specifications that were first assessed in 2017 and 2018 and therefore had five years’ data, were included) schools and colleges
- whose self-declared centre type designation stayed the same throughout 2018 to 2023 on a subject-by-subject basis, schools/colleges that had entries in the subject in each of the years 2018 to 2023
These inclusion criteria ensured that our analyses were carried out on as stable successive cohorts as possible. This was necessary for a meaningful equalities analysis as it minimises between-year changes in group differences being caused by between-year cohort changes.
Tables 1 and 2 show the number of entries by target-age candidates, centres and subjects in the resultant dataset for A level and GCSE, respectively. Values have been rounded to the nearest 5.
Modelling overview
We carried out linear mixed-effects modelling on 3 performance measures:
- mean numeric grade (for A level, grades A* to E were converted to 6 to 1 respectively and U treated as 0 while for GCSE, grades on 9 to 1 scale were numeric and U was treated as 0)
- probability of attaining A level grade A and above / GCSE grade 7 and above
- probability of attaining A level grade C and above / GCSE grade 4 and above
Each analysis took exam entry as the unit of analysis and aimed to model the relationship, in a particular year, between:
- an entry’s numeric grade or
- probability of attaining the key grades listed above or higher
The analysis also controlled for background information about the student that the entry belonged to. The full model specification can be found in Appendix D, along with a full list of model variables and their definitions in Appendix A. Interactions were not included in the models.
Using this modelling we can estimate the result for an ‘average’ entry, that is, an entry by a student who was in the reference category of every one of the background variables. In numeric grade analyses, we estimate the grade an average entry would receive. In grade probability analyses, we estimate the probability that an average entry would be awarded the key grade or above in question.
We can also estimate the size of the difference in outcome between a particular group and the reference group after controlling for effects of other background variables. For example, in the analysis on the probability of attaining grade A and above in A level in 2018, on the gender variable, an estimate of 0.0341 for male suggests that after controlling for other background variables, in 2018 male students were, on average, 3.41 percentage points more likely to achieve a grade A or above than female students (the reference category of the gender variable). Variation of these group estimates from the models covering each of the 6 years tells us how that group’s results relative to the relevant reference group have changed across the 6 years.
There is some degree of uncertainty present in any estimation arising from modelling, so to aid interpretation, 95% confidence intervals are presented in bar graphs below. For further information of how the confidence intervals were generated, see Appendix E.
Notable change criteria
We used a multi-step method for evaluating changes in relative outcome differences between key years of comparison, with the aim of identifying practically significant changes while taking into consideration normal between-year fluctuations. We used this method to evaluate changes in relative outcome differences between 2019 and 2023, and then repeated the process to evaluate changes between 2022 and 2023. This is described below.
Step 1: identify subgroups whose relative outcome differences were not significantly different from zero (at 5% level of significance) in any year and exclude them from further consideration. This step identifies the subgroups that showed no difference in any year relative to the reference group and those whose estimates consistently had large standard errors and confidence intervals, suggesting the groups were too small in size and/or had much variability within the subgroup, making it hard for their relative outcome difference to be estimated reasonably precisely.
Step 2: from the subgroups not excluded in Step 1, identify those whose 2019 to 2023 and 2022 to 2023 change in relative outcome difference in absolute value was larger than their 2018 to 2019 change in absolute value. This step considers how the relative outcome differences can change between 2 normal years, namely, 2018 and 2019, and identifies between-year changes that exceed normal between-year changes in magnitude.
Step 3: from the subgroups identified in Step 2, flag as ‘notable’ the subgroups whose 2019 to 2023 and/or 2022 to 2023 change exceeded an effect size criterion, which we set at 0.1 grade for the numeric grade measure and 1 percentage point for the grade probability measures.
To appreciate what is meant by a change between 2 years of 0.1 grade in relative outcome difference, we can consider a theoretical scenario comparing left- and right-handed students. If we had 2 groups of 100 students. Students in one group are left-handed and students in the other group are right-handed. The 2 groups are otherwise perfectly matched in background, and all take one A level subject in one year. If in one year, all 100 right-handed students receive grade B, and in the left-handed group, 50 receive grade A and 50 receive grade B, the overall difference between the groups is half a grade (0.5 grade). If the following year, the right-handed students all receive grade B, but in the left-handed group, 60 get grade B and 40 get grade A, the overall difference between the groups is slightly less than half a grade (0.4 grade) and the change between the years is 0.1 grade. There are, however, many different ways to get the same size of overall change. In the example above, a change of 0.1 grade between the years would also occur if, in the left-handed group in the second year, 5 students got an A*, 50 got an A and 45 got a B.
Vocational and Technical Qualifications Methodology
Data
The analysis includes vocational and technical qualifications (VTQs) included in the Department for Education’s performance tables, specifically Level 1, Level 1/ 2 and Level 2 Technical Awards and Technical Certificates, and Level 3 Applied Generals and Tech Level qualifications.
We evaluated the impact of each demographic and socioeconomic characteristic on students’ results this year, once other factors were controlled for. This allows us to examine the differences in attainment associated with gender, ethnicity and socioeconomic status, once other factors are controlled for, and how they have changed over several consecutive years from 2018 to 2023.
We focused on the students’ achievement of top grades rather than other points of the grading scale. The variety of grading scales used in these VTQs makes it difficult to select a meaningful and consistent midpoint. Additionally, if we were to break the analysis down by the different grading scales, the numbers would likely be too small to allow for meaningful statistical interpretation.
By ‘top grades’ we mean the single highest or best grade that can be achieved in each qualification, which will depend upon the particular grading structure that has been adopted.
We used data collected from 18 awarding organisations for 598 qualifications (not including any separate routes or pathways within those qualifications). We also obtained data on prior attainment from awarding organisations, and we used data from the Individualised Learner Record (ILR, maintained by the Education and Skills Funding Agency) and from the National Pupil Database (NPD, controlled by the DfE). These additional datasets were matched with the awards data. We used student first name, last name, date of birth, gender, qualification number and/or Unique Learner Number (ULN) to match the records for each student across the datasets. For cases which could not be uniquely matched, and those which could be matched but had no relevant information available on student characteristics of interest, we reported missing values in the corresponding fields of the combined datasets.
We analysed the qualification-level grades awarded to all students in centres in England who took assessments for these qualifications throughout the academic year. This is a change from previous analyses which included results from Spring and Summer only. This update has been made to data from all years included in this analysis.
For ethnicity, categorisations were harmonised between the NPD and ILR for consistency and to align with the Government Statistical Service guidance [List of ethnic groups - GOV.UK (ethnicity-facts-figures.service.gov.uk)] where possible. This meant some groups were merged with one of the ‘other’ groups, as numbers were too small to include as a separate category. For example, ‘Gypsy or Irish Traveller’ students were merged into the ‘Any Other White Background’ group.
Missing data rates are given in Appendix D. Data on prior attainment and the background variables are missing to varying degrees. The table in appendix D shows the extent of missing data for each background variable used in our analysis. There was little missing data on gender, but data on prior attainment and other background variables were missing to varying degrees.
Where data was missing, we included the categories in the model as ‘unknown’ groups. We did observe some notable differences (see notable difference methodology below) in some of these ‘unknown’ groups, which could indicate some degree of systematic change underlying the missing groups. The outcomes for the unknown categories are included in the tables in the results sections and in the charts in appendices.
We observed notable changes in the average marginal effects (see Modelling Overview) for the unknown categories for the following variables:
- FSM – for Technical Certificates
- gender – for Technical Awards and Tech Levels
- IDACI – for Technical Certificates
Modelling overview
We used a generalised linear model (mixed effect logistic regression) to examine the probability of attaining a top grade, given the information on the characteristics of students clustered across centres . The student characteristics described previously were treated as fixed effects, and the student’s centre was treated as a random effect. This is because there may be factors affecting results that only students from the same schools or college have in common, such as the teaching materials used. The full model specification is given in Appendix D.
Within the logistic regression model, the estimates of the fixed effects’ parameters are of most interest for our analyses. These estimates quantify the relationship between each demographic or socioeconomic characteristic as well as prior attainment and the probability of attaining a top grade. Prior attainment is a strong predictor of grades and should be presented alongside the demographic or socioeconomic characteristics to facilitate a more accurate interpretation of effect size of variables.
Multi-way interactions between the demographic and socioeconomic variables listed above as well as prior attainment were not included in the analysis. This is because the small sample sizes would make the results less meaningful.
For each year separately, we show a measure of effect size of each variable on the probability of achieving the top grade. This is expressed in the form of the average marginal effect, representing an average difference in the probability of achieving top grades between two categories of a demographic or socioeconomic characteristic.
For example, the average marginal effect for gender shows how the average probability of achieving the top grade differs for male students (category of interest) compared to female students (reference category) when the remaining variables (other categories) are held constant. Through these measures, we can assess the difference in relative achievement of the top grade between different demographic groups.
Notable change criteria
Logistic regression models were run for each year individually. We then evaluated their outputs to identify which effects have changed between key years of comparison, considering both the statistical significance and the meaningfulness of the effects. We used a multi-step method (similar to that used for GQ analyses) to evaluate changes in effects between 2019 and 2023, and then repeated the process to evaluate changes between 2022 and 2023. The method consists of the following steps:
Step 1: identify which subgroups of students were statistically significantly more or less likely to achieve the top grade than the reference category in any year. That is, where the average marginal effects were statistically significantly different from zero (at 5% level of significance). Include the identified subgroups for consideration in subsequent steps. This step allows us to exclude from further investigation those subgroups that showed no difference in any year relative to the reference group and those whose estimates consistently had large standard errors and confidence intervals, suggesting the groups were too small in size and/or had much variability within the subgroup, making it hard for their effect difference to be estimated reasonably precisely.
Step 2: among the subgroups identified in Step 1, select those whose difference in the average marginal effects between 2019 and 2023 in absolute value was larger than the difference in average marginal effects between 2018 and 2019 in absolute value. This step considers how the size of the average marginal effects can change between two normal years, namely, 2018 and 2019, and identifies between-year changes that exceed normal between-year changes in magnitude.
Step 3: from the subgroups selected in Step 2, flag as ‘notable’ the subgroups whose 2019 to 2023 change in the average marginal effects was larger than plus or minus 5 percentage points.
The purpose of the method is to ensure that changes are only interpreted as being ‘notable’ if they appear to be larger than the normal fluctuations that might be expected in any year. However, smaller changes will also be discussed in the sections to follow where they are apparent in the graphs.
For any feedback on these graphs, please contact [email protected].
Return to the Ofqual Analytics home page.
If you need an accessible version of this information to meet specific accessibility requirements, please email [email protected] with details of your request.
What do the charts show?
The analysis below shows how results for different groups of students have changed over time for GCSEs and A levels, when controlling for other variables. The charts display results gaps for students with a chosen characteristic when compared to students from a reference group.
Our analysis uses multivariate regression modelling, so we can measure the impact of each of the students’ characteristics considered once all others have been held constant. For example, we can compare the results of 2 different ethnic groups, without differences in their overall prior attainment or socio-economic make-up affecting the findings.
For most of the variables, the largest group is used as a comparator, and all other groups are compared to that. For example, for ethnicity, we use white British as the comparator as it is the largest group. We compare students in other ethnic groups with white British students of the same gender, special educational meals status, free school meals eligibility, Income Deprivation Affecting Children Index score, prior attainment, first language, region and centre type. We estimate the results of the ‘average’ student, that is, a student who falls into the comparator group for every variable, and can then examine the impacts of each of the other groups separately.
For further detail on the methodology used, please see the background and methodology tab.
What do the different options mean?
Select from the drop down menus whether you would like to see analysis for A levels or GCSE, and from the different groups included in the analysis. You can also choose whether you would like to see outcomes at average grade (numeric grade) level or probabilities at particular grades. For the numeric grade measure, for A level, grades A* to E were converted to 6 to 1 respectively and U treated as 0 while for GCSE, grades on 9 to 1 scale were numeric and U was treated as 0.
You can then choose to display:
- the outcomes from the statistical modelling, shown as bars, where results take into account other variables included in the analysis; and/or
- raw outcomes shown as points, which are the averages, or the differences of the averages from the reference group, for each sub-group without controlling for other variables.
Finally, you can also choose whether to view:
- the differences relative to the reference group; or
- the overall absolute estimates.
2019 to 2023 notable changes
2022 to 2023 notable changes
For any feedback on these graphs, please contact [email protected].
Return to the Ofqual Analytics home page.
If you need an accessible version of this information to meet specific accessibility requirements, please email [email protected] with details of your request.
What do the charts show?
The analysis below shows how results for different groups of students have changed over time for VTQs included in the Department for Education’s performance tables, specifically Level 1, Level 1/ 2 and Level 2 Technical Awards and Technical Certificates, and Level 3 Applied Generals and Tech Level qualifications, when controlling for other variables. The charts display results gaps for students with a chosen characteristic when compared to students from a reference group in terms of average probabilities of achieving top grades.
Our analysis uses multivariate regression modelling, so we can measure the impact of each of the students’ characteristics considered once all others have been held constant. For example, we can compare the results of 2 different ethnic groups, without differences in their overall prior attainment or socio-economic make-up affecting the findings.
For most of the variables, the largest group is used as a comparator, and all other groups are compared to that. For example, for ethnicity, we use white British as the comparator as it is the largest group. We compare students in other ethnic groups with white British students of the same gender, special educational needs status, free school meal eligibility, Income Deprivation Affecting Children Index score and prior attainment. We estimate the results of the ‘average’ student, that is, a student who falls into the comparator group for every variable, and can then examine the impacts of each of the other groups separately.
For further detail on the methodology used, please see the background and methodology tab.
What do the different options mean?
Select from the drop-down menus whether you would like to see analysis for Level 1, 1/ 2 and 2, or Level 3 qualifications, the qualification group and from the different groups included in the analysis.
You can then choose which outcomes should be displayed. A default ‘Modelled’ option, shown as bars, shows results in which all the remaining student’s characteristics are taken into account . The ‘Raw’ option, shown as points, will show outcomes which are the raw percentage point differences between the average for each sub-group and the reference group without controlling for any other variables.
2019 to 2023 notable changes
2022 to 2023 notable changes
For any feedback on these graphs, please contact [email protected].
Return to the Ofqual Analytics home page.
If you need an accessible version of this information to meet specific accessibility requirements, please email [email protected] with details of your request.
All models fitted can be expressed mathematically as:
where
All analyses included student, centre and subject as random effects, to take account of students taking multiple subjects and students clustering within centres. The subject random effects had the following categories:
-
A level: Art & Design: 3D Studies, Art & Design: Art, Craft and Design, Art & Design: Critical and Contextual Studies, Art & Design: Fine Art, Art & Design: Graphics, Art & Design: Photography, Art & Design: Textiles, Biology, Business Studies, Chemistry, Classical Greek, Computing, Dance, Drama & Theatre Studies, Economics, English Language, English Language & Literature, English Literature, French, Geography, German, History, Latin, Music, Physical Education, Physics, Psychology, Religious Studies, Sociology, Spanish
-
GCSE: Art & Design: 3D Studies, Art & Design: Art, Craft and Design, Art & Design: Critical and Contextual Studies, Art & Design: Fine Art, Art & Design: Graphics, Art & Design: Photography, Art & Design: Textiles, Biology, Chemistry, Citizenship Studies, Classical Greek, Combined Science, Computing, Dance, Drama, English Language, English Literature, Food Prep and Nutrition, French, Geography, German, History, Latin, Mathematics, Music, Physical Education, Physics, Religious Studies, Spanish
The fixed effects of the models were: (please refer to the tables available on the results page for keys to the acronyms and abbreviations)
- Gender: male, female (reference category) (the unknown/neither category was omitted in the modelling because of the extremely small number of entries belonging to the category)
- Ethnicity: ABAN, AIND, AOTH, APKN, BAFR, BCRB, BOTH, CHNE, MOTH, MWAS, MWBA, MWBC, WBRI (reference category), WIRI, WIRT (only in GCSE analyses), WOTH (subsuming WIRT and WROM in A level analyses), WROM (only in GCSE analyses), unknown
- Major language: English (reference category), NotEnglish, unknown
- SEND status: NoSEND (reference category), SEND, unknown
- FSM eligibility: NoFSM (reference category), FSM, unknown
- Deprivation: very low, low, medium (reference category), high, very high, unknown
- Prior attainment: very low, low, medium (reference category), high, very high, unknown
- Centre type: Acad (reference category), Free, FurE, Indp, Other, SecComp, SecMod, SecSel, Sixth. In a change from previous analyses, Tert (tertiary) was collapsed into FurE for all years.
- Region: EM, EA, LD, NE, NW, SE (reference category), SW, WM, Y&H
For the grade probability measures, we also ran logistic regressions in which the dependent variable yijk was the natural logarithm of the odds of the exam entry by candidate i in centre j in subject k being awarded the target grade. The exponentials of the β coefficients of a fitted logistic regression model are the odds ratios between groups which can be interpreted as estimates of the likelihood of entries by students of a particular group being awarded the target grade relative to entries by students of the reference group after controlling for other variables. For the between-group comparisons examined in our modelling, the pattern of changes in odds ratio across the years in the logistic models was consistent with the pattern of changes in relative outcome difference across the years in the linear probability models. We present results of the linear models for the grade probability measures in this report, as probabilities are more intuitive to interpret than odds ratios, but a drawback of the linear models should be noted, which is that some high performing subgroups have modelled probability estimates and/or the upper limits of the 95% confidence intervals of those estimates larger than the theoretical maximum of 1.
An accessible version of this document is available here
A mixed effect modelling approach was also adopted for VTQ analysis, whereby the learner characteristics (including their prior attainment) were treated as fixed effects, and the learner’s centre was treated as a random effect. This is because there may be factors affecting results that only learners from the same centre have in common, such as teaching materials used at their school or college.
The logistic regression specification used for modelling takes the form:
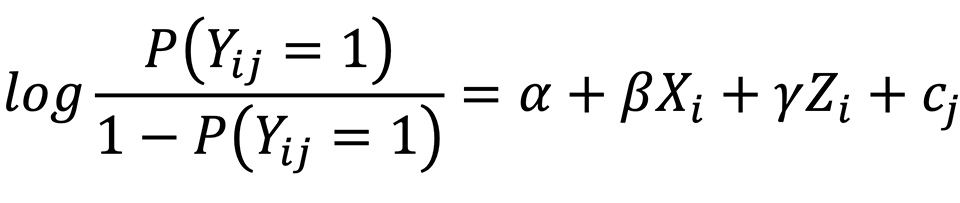
where:
All β coefficients had associated standard errors (SEs), which quantified how precisely β coefficients had been estimated. The SEs were used to compute the 95% confidence intervals (CIs) of the β coefficients, using the formula: 95% CI = β ± 1.96*SE. βs (taken as estimates of relative outcome differences after controlling for other background variables). The same calculation was used for both GQ and VTQ analyses.
For any feedback on these graphs, please contact [email protected].
Return to the Ofqual Analytics home page.
If you need an accessible version of this information to meet specific accessibility requirements, please email [email protected] with details of your request.